Az előadás vázlata:

1. A kompetencia alapú oktatás általános jellemzői mennyiben érvényesülnek a matematikai kompetencia fejlesztésében?

2. Milyen specialitásai vannak a matematikai területnek?

Kompetencia:
Az ismeretek, azok alkalmazási képessége és az alkalmazáshoz szükséges megfelelő motivációt biztosító attitűdök összessége.

Kompetencia alapú oktatás:
a képességek, készségek fejlesztését, az alkalmazásképes tudást helyezi a középpontba.

Feltétele: a pedagógiai módszertani kultúra megújítása.
Főbb eszközei: a problémaközpontú tanítás, a cselekvésből kiinduló gondolkodásra nevelés, a felfedeztető tanítás-tanulás, a megértésen és tevékenységen alapuló fejlesztés.

Mikor, miért, hogyan került előtérbe a kompetencia alapú oktatás?

2001 EU ajánlások
A gazdaság igényei: olyan ismereteket, amelyeket közvetlenül alkalmazni lehet.
A megnövekedett létszám a középiskolákban. A fejlődésben mutatkozó egyre nagyobb különbségek.
Az információs források gyors változása:TV, mobil, internet, számítógép.
Az OECD PISA-vizsgálatok kapcsán döbbent rá jó néhány oktatási kormányzat arra, hogy az alapkompetenciákat jobban kell gondozni az oktatás folyamán, s ez a felismerés hatott arra, hogy a kompetencia fogalmának értelmezésével s magával a kompetencia alapú oktatás sajátosságaival el kezdett foglalkozni a pedagógiai szakma (Pála Károly)

A PISA-sokk szimbóluma matematikából:
2002 október 9. évfolyam

1. feladat
P1m154Q01- 0 1 6 7 8 9
Egy pizzériában két fajta kerek pizzát árulnak. Ezek vastagsága azonos, de átmérőjük különböző. A kisebbik 30 cm átmérőjű, és 30 tallérba kerül, a nagyobbik 40 cm átmérőjű, és 40 tallérba kerül. Melyik pizza éri meg jobban az árát? Válaszodat indokold!
Az árak aránya: 4:3, a területek aránya: 16:9
De 16/9 > 4/3 = 12/9 , tehát a kisebb egységára a nagyobb.

Mit értünk a matematikai kompetencián?

A matematikai kompetencia

• a matematikai tantárgyi ismeretek,
• a matematikai készségek és képességek,
• általános készségek és képességek,
• motívumok és attitűdök

együttese.

Mik a legfőbb módszertani alapelvek?

A matematika tanulása a cselekvő, személyes tapasztalatszerzéssel kezdődik, ehhez eszközökre van szükség.
A matematikai problémák játékba ágyazása alkalmas formája a fejlesztő, nevelő munkánknak
A problémafelvetés lehetőleg életszerű helyzetekből indul ki.
Az alkotó gondolkodásra csak alkotások létrehozásával nevelhetünk.

Milyen vezérelvek szerint állítottuk össze programcsomagot?

Az 1 - 12. évfolyamig:

• egységes szemlélet
• azonos alapelvek
• összefüggő tanulási-tanítási folyamat

A kompetencia fejlesztés komplex folyamat:

ismeretszerzés
képességfejlesztés

együttese.

Hogyan épült fel a program tartalma?

Matematikai tevékenységek rendszere

• életkori sajátosságok
• egyéni sajátosságok

A fogalmi építkezés folyamata .

Tapasztalatszerzés, problémafelvetés gyakorlat, életszerű helyzetek játék

Elemzés, összegezés

A gyakorlat és elmélet kétirányú útja

A motiváció eszközei

Belső motiváció:

• játékok, eszközök
• a kitalálás izgalma,
• az alkotás öröme,
• matematikatörténeti érdekességek,
• csoportos kutatómunkák,
• kooperatív tanulási technikák
• számítógép használata

Igaz vagy lehetséges legyen minden állítás!

• Kati rajzolt a füzetébe egy 52____ hosszú vonalat.
• Zoli szobája 52_____ hosszú.
• Juli vonattal utazott nagymamájához, aki 52_____ -re lakik tőlük.
• Zsolti bátyja már hatodikos, 52_____ a tömege.
• Anya a leveshez 52_____ gombát vett.
• Minden nap iszom egy bögre kakaót, tehát egy hónap alatt biztosan elfogyasztok 52_____-t.
• Kb. 52_____ alatt tudom elénekelni a Kis kece lányom hét versszakát.
• 52_____ múlva még mindig szeptember lesz.
• 52_____ múlva még mindig harmadikosok leszünk.

Igaz vagy lehetséges legyen minden állítás!

Egy gyalogos egyenletesen haladva sétál egyenes úton. Átlagosan 50 m-t tesz meg 1 perc alatt a nyíl irányában.

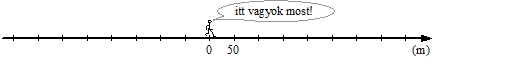
Egy gyalogos egyenletesen haladva sétál egyenes úton. Átlagosan 50 m-t tesz meg 1 perc alatt a nyíl irányában.

A konkrét tartalom kiválasztásának szempontjai

Szerethető
Megbízható
Tanulható és tanítható

Titkosírás 9. évfolyam, függvények

Kiderült, hogy az üzenetek küldője Abe Slaney, a legveszélyesebb bűnöző Chicagoban. Halálosan megfenyegette Elsiet, aki Amerikában a kedvese volt, de megszökött tőle. Sajnos Holmesnak nem sikerült megakadályoznia a tragédiát, de a kódot felhasználva sikerült elcsípni, és börtönbe juttatni a bűnözőt. A következő üzenetet küldte neki:

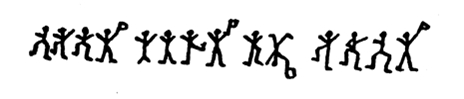
COME HERE AT ONCE (Gyere ide azonnal)
Slaney gyanútlanul átment a birtokra, ahol Holmes már rendőri kísérettel várta. Holmes a kód megfejtéséhez a gyakorisági analízist használta, ugyanis rájött arra, hogyminden emberke egy-egy betűt kódol. (Nem szavakat, nem szótagokat).

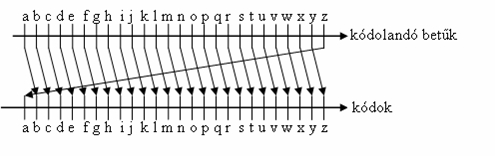
Az ilyen eljárások közül a legegyszerűbb talán a Ceasar-kód, mely Julius Ceasarról kapta a nevét. Lényege, hogy egy betű helyére mindig a közvetlenül rákövetkezőt írjuk. Az utolsó betű helyére pedig az ábécé első betűje került. Ez az eljárás olyan, mintha az ábécételcsúsztatnánk egy betűvel. Ezt ábrázolja a következő nyíldiagram az angol ábécé kisbetűire:

A magyar matematikatanításban mindig is létezett a kompetenciaszemlélet és kompetencia-központúság , más formában, más szóhasználattal.

Varga Tamás: A kivételesek vannak többen.1972

100 tizenkétéves gyerek közül

mindössze 20 gyerek mentális kora azonos az életkorával, 80 (!) gyereké ettől eltérő.

Varga Tamás: A kivételesek vannak többen.1972

Varga Tamás
„A matematika a legalsóbb szinttől a legfelsőig tapasztalatokból nő ki: próbálkozásokból, sejtésekből és ellenőrzésükből, elvetésükből vagy megerősítésükből. Mégis az emberi szellem szabad alkotása. Híd a két kultúra között. Tele van játékossággal, esztétikummal: művészet is”
 

Péter Rózsa:
"Én így képzelem: a matematika forrása, vagy legalább is egyik forrása az ember játékos természete és éppen ezért nemcsak tudomány a matematika, hanem legalább ugyanolyan mértékben művészet is."

Rényi Alfréd:
„Aki azt mondja, nem szereti a matematikát, az tulajdonképpen azt mondja, nem szeret gondolkozni.”

A szimmetria fogalma

Egy alakzat tengelyesen szimmetrikus (tengelyesen tükrös), ha van olyan tengelyes tükrözés, ami az alakzatot önmagába viszi.

Egy alakzat középpontosan szimmetrikus (középpontosan tükrös), ha van olyan középpontos tükrözés, ami az alakzatot önmagába viszi.

Vannak alakzatok, amelyek mindkét szimmetriatulajdonsággal rendelkeznek.

Rényi Alfréd: Dialógusok a matematikáról:

Szókratész: Gondolj csak arra, hogy a matematika elvont fogalmai hogyan jöttek létre. Azt mondottuk, hogy amikor a matematikus a számokkal foglalkozik, nem a juhok vagy a hajók számára gondol, hanem a számokra általában, elvonatkoztatva attól, hogy milyen dolgok számáról van szó. De képes erre az elvonatkoztatásra az, aki még nem számolt meg kézzel fogható, létező dolgokat? Amikor a gyereket számolni tanítják, először kavicsok vagy pálcikák megszámolására tanítják őket. Csak ha már a gyerek meg tud számolni kavicsokat és pálcákat, akkor képes eljutni odáig, hogy megértse, nemcsak két kavics és három kavics az öt kavics, hanem, hogy két valami és három valami az mindig öt valami, vagyis hogy kettő meg három az öt. Nem más a helyzet a geometriai formákkal sem. A gömb fogalmához is csak úgy juthat el a gyerek, hogy először labdákat és más gömbölyű testeket ismer meg, és ezekből a tapasztalataiból szűri le a gömb elvont fogalmát. És nemcsak a gyermekeknél van ez így, hanem így alakultak ki a múltban a matematika összes alapvető fogalmai: lassan és fokozatosan.

Surányi János: „Harmadik elemista voltam, amikor tanítóm megmutatta, hogyan lehet azt bizonyítani, hogy a háromszög szögeinek összege 180°. Nem a tény fogott meg, hanem az, hogy ezt be is lehet bizonyítani. Ez keltette fel érdeklődésemet a matematika iránt. Az elemiben matematikával nem nagyon találkoztunk, csak számolással, bár számolni nagyon szerettem.” „Szerintem a középiskolában is úgy kell tanítani, hogy valami perspektívát kell adni. Nem az a lényeg, hogy tételek tömegével tömjük a diákokat, hanem az, hogy megtanuljanak gondolkodni. A tanítás során rá kell mutatni az egyes témakörök kapcsolataira.”

Lovász László
(Origo interjú 2006)

… „a tévhittel ellentétben a matematika nem lezárt, hanem folyamatosan változó, fejlődő, élő tudomány, amely minden területen befolyásolja az életünket. Az egzakt gondolkodás kialakításához pedig egyszerűen nélkülözhetetlen.” … „a magyar tudomány jellege már legalább száz éve nem követő, provinciális, hanem nemzetközi színvonalú, és óriási felelősségünk van ennek megőrzésében.”

Mindentudás Egyeteme 2003 Lovász László

„Napjainkban teljesen magától értetődőnek tűnik, hogy munkánk során számítógépet használunk, internetezünk, bankkártyával fizetünk vagy meghallgatunk egy CD-lemezt. Ilyenkor talán végig sem gondoljuk, hogy ezek egyikét sem tehetnénk meg, ha nem jöttek volna létre a matematika új ágai: az algoritmuselmélet, a kriptográfia vagy a bonyolultságelmélet.”

Klasszikus kérdések új megvilágításban

A klasszikus matematikát sokan elefántcsonttoronynak látják. Godfrey Hardy, aki a prímszámok elméletének egyik legkiemelkedőbb kutatója volt a 20. század első felében, ezt írja Egy matematikus védekezése című könyvében:

Soha nem tettem semmi ,,hasznosat”. Semelyik felfedezésem sem volt közvetlenül vagy közvetve jó vagy rossz hatással a világ folyására, és nem valószínű, hogy valaha is hatással lesz...

Az ,,igazi" matematikusok ,,igazi" matematikája, Fermat és Euler és Gauss és Abel és Riemann matematikája csaknem teljesen ,,haszontalan'' kérdések

Amikor az interneten vásárolunk vagy bankügyeket intézünk, számítógépünknek több száz jegyű számokról kell eldöntenie, hogy primek-e – tizedmásodpercek alatt. Ehhez Fermat tételét használja. A különböző számítógépes protokollok, biztonsági módszerek a Hardy által felsorolt nagyságok szinte mindegyikének a munkájára építenek.

Ha azt kérdezzük, hogy melyik az a megoldatlan matematikai probléma, melynek a legnagyobb a gyakorlati jelentősége, azt hiszem, egyértelmű a válasz: Fel lehet-e egy mondjuk 1000 jegyű számot hatékonyan (nem-csillagászati idő alatt) prímtényezőire bontani?

Azt hiszem azonban, hogy ezek a tények Hardy kutatási elveit legalább annyira alátámasztják, mint amennyire az állításait cáfolják. Ha ezeket a nagyságokat csak kutatásuk közvetlen haszna motiválta volna és nem a matematikai kérdések szépsége, a megismerés vágya, akkor ma nem lennének eszközeink a számítógép-rendszerek biztonságának védelmére.”

Láttassuk be a gyerekekkel, hogy a prímeknek kitüntetett szerepe van az egészek között, mivel minden pozitív egész szám felépíthető prímekből és az 1-ből szorzással.

Ahogyan a kőműves a téglákat malterral tapasztja össze, mi a prímtégláinkat szorzással „tapasztottuk össze”. Minden prím egy építőkő és minden szám egy épület, amelyet prímtéglából szorzás segítségével építettünk.

a) Feltettem arccal lefelé két prímkártyát.
Gyűjtsünk róla igaz állításokat! összetett szám; ez a szám legalább 4; lehet, hogy négyzetszám; lehet, hogy ez 1 milliónál nagyobb; stb.,

b) Ha tudnánk erről a számról, hogy a prímtégláiból csak két különböző számot tudnánk építeni, akkor mit mondhatnánk a tégláiról? a két prímtégla azonos

c) Ha tudnánk erről a számról, hogy a két prímtéglája különböző, akkor hány különböző számot tudnánk belőlük építeni? hármat

d) Eláruljuk, hogy ez egy páros négyzetszám. Mi van a kártyákon? két 2-es